Swirl function
In mathematics, swirl functions are special functions defined as follows[1]:
where k and n are integers, and r and θ are polar coordinates.
When these functions are graphed, they usually resemble a swirling fan blade, where n is the number of blades, k is related to the shape of each blade.
Symmetry
The function S(k,n,r,θ) satisfies the following relations:
- mirror symmetry
- full symmetry
- rotation symmetry
examples
First number is n, second is k
 7,-2
7,-2 7,2
7,2 7,-4
7,-4 7,4
7,4 7,-6
7,-6 7,6
7,6 7,-8
7,-8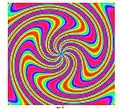 7,8
7,8 7,-10
7,-10 7,10
7,10 7,-12
7,-12 7,12
7,12
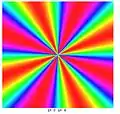 0,4
0,4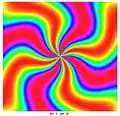 1,4
1,4 2,4
2,4 7,4
7,4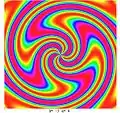 -5,4
-5,4 -9,4
-9,4 30,4
30,4
References
- Trott, M. Graphica 1: The World of Mathematica Graphics. The Imaginary Made Real: The Images of Michael Trott. Champaign, IL: Wolfram Media, pp. 36–37 and 86, 1999.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.