Snub icosidodecadodecahedron
In geometry, the snub icosidodecadodecahedron is a nonconvex uniform polyhedron, indexed as U46. It has 104 faces (80 triangles, 12 pentagons, and 12 pentagrams), 180 edges, and 60 vertices.[1] As the name indicates, it belongs to the family of snub polyhedra.
| Snub icosidodecadodecahedron | |
|---|---|
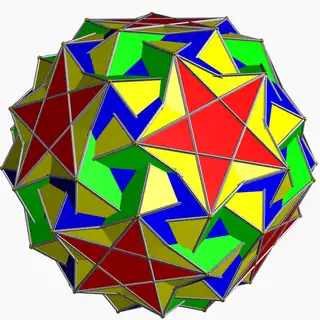 | |
| Type | Uniform star polyhedron |
| Elements | F = 104, E = 180 V = 60 (χ = −16) |
| Faces by sides | (20+60){3}+12{5}+12{5/2} |
| Wythoff symbol | | 5/3 3 5 |
| Symmetry group | I, [5,3]+, 532 |
| Index references | U46, C58, W112 |
| Dual polyhedron | Medial hexagonal hexecontahedron |
| Vertex figure |  3.3.3.5.3.5/3 |
| Bowers acronym | Sided |

3D model of a snub icosidodecadodecahedron
The circumradius of the snub icosidodecadodecahedron with unit edge length is
where ρ is the plastic constant, or the unique real root of ρ3 = ρ + 1.[2]
Related polyhedra
Medial hexagonal hexecontahedron
| Medial hexagonal hexecontahedron | |
|---|---|
 | |
| Type | Star polyhedron |
| Face |  |
| Elements | F = 60, E = 180 V = 104 (χ = −16) |
| Symmetry group | I, [5,3]+, 532 |
| Index references | DU46 |
| dual polyhedron | Snub icosidodecadodecahedron |

3D model of a medial hexagonal hexecontahedron
The medial hexagonal hexecontahedron is a nonconvex isohedral polyhedron. It is the dual of the uniform snub icosidodecadodecahedron.
See also
References
- Maeder, Roman. "46: snub icosidodecadodecahedron". MathConsult.
{{cite web}}: CS1 maint: url-status (link) - Weisstein, Eric W. "Snub icosidodecadodecahedron". MathWorld.
- Wenninger, Magnus (1983), Dual Models, Cambridge University Press, ISBN 978-0-521-54325-5, MR 0730208
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.