Hole (topology)

In topology, a hole is, informally, a "missing ball". More formally, a topological space has a hole if it contains a sphere that cannot be continuously extended to a ball. Equivalently, it contains a sphere that cannot be shrunk into a single point by a continuous transformation.[1]^: 78 If the sphere is a copy of the d-dimensional sphere S^d (so the missing ball is a copy of the (d+1)-dimensional ball B^d+1), then one can say that the hole has a d-dimensional boundary (or that the hole is (d+1)-dimensional).

Definitions

Let X be a topological space. A d-dimensional sphere in X is a continuous function $f_{d}:S^{d}\to X$ . A d-dimensional ball in X is a continuous function $g_{d}:B^{d}\to X$ .

If there is a d-dimensional sphere that cannot be extended to a (d+1)-dimensional ball, then X has a (d+1)-dimensional hole. Informally, the (d+1)-dimensional ball that would have been bounded by the sphere is missing from the space. Note: some authors call such a hole a d-dimensional hole, but it is more natural to say that the dimension of the hole is the dimension of the "missing" ball, which is d+1.

Equivalent definition: If there is a d-dimensional sphere $f_{d}$ that is not null-homotopic (- there is no homotopy from $f_{d}$ to a constant function $h_{d}:S^{d}\to \{x_{0}\}$ , for some point $x_{0}\in X$ ), then X has a (d+1)-dimensional hole. Informally, the sphere cannot be shrunk continuously to a single point in X.

A 2-dimensional hole (a hole with a 1-dimensional boundary).

Examples

2-dimensional holes

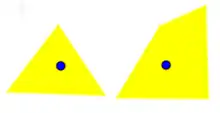
A 2-dimensional hole (a hole with a 1-dimensional boundary) is a circle (S¹) in X, that cannot be shrunk continuously to a point in X. An example is shown on the figure at the right. The yellow region is the topological space X; it is a pentagon with a triangle removed. The blue circle is a 1-dimensional sphere in X. It cannot be shrunk continuously to a point in X; therefore; X has a 2-dimensional hole. Another example is the punctured plane - the Euclidean plane with a single point removed, $\mathbb {R} ^{2}\setminus \{(0,0)\}$ . To make a 2-dimensional hole in a 3-dimensional ball, make a tunnel through it.[1] In general, every topological space that is not simply-connected has a 2-dimensional hole.

A 3-dimensional hole.

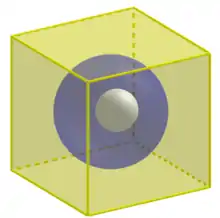
3-dimensional holes

A 3-dimensional hole (a hole with a 2-dimensional boundary) is shown on the figure at the right. Here, X is a cube (yellow) with a ball removed (white). The 2-dimensional sphere (blue) cannot be continuously shrunk to a single point.

A 1-dimensional hole.

1-dimensional holes

For a 1-dimensional hole (a hole with a 0-dimensional boundary) we need to consider $S^{0}$ - the zero-dimensional sphere. What is a zero dimensional sphere? - For every integer d, the sphere $S^{d}$ is the boundary of the (d+1)-dimensional ball $B^{d+1}$ . So $S^{0}$ is the boundary of $B^{1}$ , which is the interval [0,1]. Therefore, $S^{0}$ is the set of two disjoint points {0, 1}. A zero-dimensional sphere in X is just a set of two points in X. If there is such a set, that cannot be continuously shrunk to a single point in X, this means that there is no path between the two points, that is, X is not path-connected; see the figure at the right. In general, every topological space that is not path-connected has a 1-dimensional hole.

0-dimensional holes

A 0-dimensional hole is a missing 0-dimensional ball. A 0-dimensional ball is a single point. Therefore, the existence of a 0-dimensional hole is equivalent to the space being empty.

Homotopical connectivity

The homotopical connectivity of a space X, denoted conn_h(X), is the largest integer d such that X contains no holes with boundary dimension at most d. A

slightly different definition of connectivity, which makes some computations simpler, is: the smallest integer d such that X contains a hole with dimension d. This connectivity parameter is denoted by $\eta _{\pi }(X)$ , and it differs from the previous parameter by 2: $\eta _{\pi }(X):={\text{conn}}_{\pi }(X)+2$ .[2]

As the above examples show:

For an empty space, $\eta _{\pi }(X)=0$ , since it has a 0-dimensional hole;
For a non-empty but not path-connected space, $\eta _{\pi }(X)=1$ , since it has a 1-dimensional hole;
For a path-connected but not simply-connected space (e.g. a circle) $\eta _{\pi }(X)=2$ , since it has a 2-dimensional hole;
For a simply-connected space (e.g. a sphere) $\eta _{\pi }(X)\geq 3$ . In general, $\eta _{\pi }(S^{d})=d+1$ .

Holes and homotopy groups

If a topological space X has no hole with a d-dimensional boundary, then - by definition - every d-dimensional sphere in X is homotopic to a constant map. Therefore, the d-th homotopy group of X is trivial. The opposite is also true: If X has a hole with a d-dimensional boundary, then there is a d-dimensional sphere that is not homotopic to a constant map, so the d-th homotopy group of X is not trivial. In short, X has a hole with a d-dimensional boundary, if-and-only-if $\pi _{d}(X)\not \cong 0$ .

References

Matoušek, Jiří (2007). Using the Borsuk-Ulam Theorem: Lectures on Topological Methods in Combinatorics and Geometry (2nd ed.). Berlin-Heidelberg: Springer-Verlag. ISBN 978-3-540-00362-5. Written in cooperation with Anders Björner and Günter M. Ziegler , Section 4.3
Aharoni, Ron; Berger, Eli (2006). "The intersection of a matroid and a simplicial complex". Transactions of the American Mathematical Society. 358 (11): 4895–4917. doi:10.1090/S0002-9947-06-03833-5. ISSN 0002-9947.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[:0-1] Matoušek, Jiří (2007). Using the Borsuk-Ulam Theorem: Lectures on Topological Methods in Combinatorics and Geometry (2nd ed.). Berlin-Heidelberg: Springer-Verlag. ISBN 978-3-540-00362-5. Written in cooperation with Anders Björner and Günter M. Ziegler , Section 4.3

[2] Aharoni, Ron; Berger, Eli (2006). "The intersection of a matroid and a simplicial complex". Transactions of the American Mathematical Society. 358 (11): 4895–4917. doi:10.1090/S0002-9947-06-03833-5. ISSN 0002-9947.